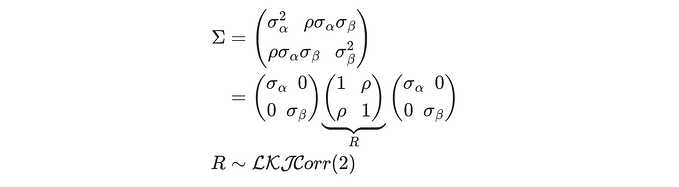Cholesky factors of covariance and correlation matrices in Stan

In this blog, I would like to give a quick overview of different types of matrices and their transformations (e.g., Cholesky decomposition) in stan. These matrices include variance-covaiance matrix (Σ), correlation matrix (R), Cholesky factor of covariance matrix (L) and Cholesky factor of correlation matrix (Lcorr). Before we move to Cholesky decomposition, it is good to know the relationship between variance-covaiance matrix (Σ) and correlation matrix (R). Simply put, we can rewrite Σ as the product of a diagonal matrix (σ) and a correlation matrix (R) in the following way. To achieve this, you can use the quad_form_diag(R, sigma) function in stan.

cov_matrix[K] Sigma = quad_form_diag(R, sigma); // variance-covariance matrix Sigma
corr_matrix[K] R; // correlation matrix R

It is important to know that we can decompose a symmetric and positive semi-definite matrix into the product of a lower triangular matrix (called Cholesky factor) and its transpose via Cholesky decomposition. As illustrated below, we can apply Cholesky decomposition either to the variance-covaiance matrix (Σ), or to the correlation matrix (R). To distinguish between these two matrices, you just need to remember that the correlation matrix has 1 whereas the variance-covariance matrix has σ^2 at the main diagonal.